이 포스팅의 목표는 필자가 알고리즘을 공부하며 습득한 내용을 정리하는 데 있습니다. 따라서 틀린 내용이 있을 수 있습니다. 틀린 내용을 발견하신 경우 댓글로 지적해 주시면 감사하겠습니다.

1. 서론
그리디Greedy 알고리즘은 단순 무식하게, 현재 상황에서 최선의 선택만을 하는 알고리즘이다. 그리디 알고리즘은 매 순간 최선의 선택만을 하므로, 이후의 상황에 대해서는 전혀 고려하지 않는다.
그리디 알고리즘은 모든 상황을 고려하는 것이 아니기 때문에 시간을 크게 절약할 수 있다. 허나 그리디 알고리즘의 유형은 매우 다양하기 때문에, 특정 문제를 만났을 때 이 문제가 그리디 알고리즘으로 해결 가능한지를 파악할 수 있어야 한다.
2. 그리디 알고리즘의 조건
그리디 알고리즘을 사용하기 위해서는 크게 2가지 조건을 만족해야 한다.
- 탐욕스러운 선택 속성(Greedy Choice Property)
현재의 선택이 이후의 선택에 영향을 주지 않아야 한다.
- 최적 부분 구조(Optimal Substructure)
전체 문제의 최적 해결 방안이 부분 문제의 최적 해결 방안이어야 한다.
위 조건이 성립하지 않는다면, 그리디 알고리즘으로 해결할 수 없다.
3. 그리디 알고리즘의 정당성
그리디 알고리즘의 최선의 선택이라는 말이 어쩌면 말이 좋게 들릴 수 있겠지만, 현재 상황에서의 최선이기 때문에 오히려 함정에 빠질 수 있다. 예를 들어 보자.
3-1. 최소 경로 문제
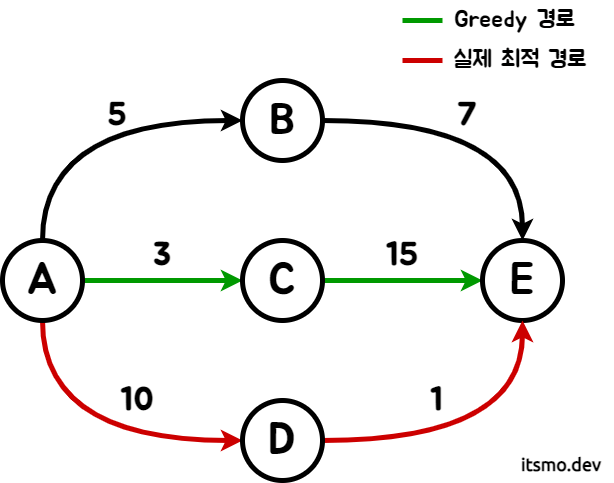
위와 같은 그래프가 있다고 가정하자. 각 노드 사이의 간선은 다음 노드까지의 거리를 나타낸다. A에서 E로 가는 최소 거리는 얼마인가? 우리는 이미 머릿속에서 모든 경우의 수를 다 더해 보았기 때문에 A-D-E가 최소 경로임을 알지만, 이를 현재 상황만 고려하는 그리디 알고리즘으로 해결한다고 생각해 보고 문제를 들여다 보자.
A에서 B/C/D 각각의 노드로 이동하는 경로 중 최소 경로는 A-C이다. 그리디는 뒷일은 고려하지 않으므로 C로 가는 길을 택할 것이다.
문제는 다음 경로에 있다. C에서 도착지인 E까지 가는 경로는 거리 15짜리 길 단 하나다. 이렇게 되면 그리디 알고리즘은 3+15인 18이 최소 경로라고 답할 것이다.
당연하지만 이 문제는 그리디 알고리즘의 첫 번째 조건을 만족하지 못하기 때문에 그리디 알고리즘으로 풀 수 없다. 첫 번째 선택이 다음 경로 선택에 영향을 주기 때문이다.
3-2. 거스름돈 문제
가장 많이 나오는 그리디 알고리즘 문제의 예로는 거스름돈 문제가 있다. 일례로 N원을 500원, 100원, 50원, 10원 화폐 단위로 거슬러 줄 때, 이 거스름돈으로 N원을 만드는 데 필요한 화폐 개수의 최솟값을 출력하는 문제가 그것이다.
해당 문제는 큰 단위의 화폐부터 차례대로 거슬러 준다면 쉽게 해결이 가능하다. 그러나 이 문제는 거스름돈의 단위를 변경했을 때 그리디 알고리즘의 조건을 만족하지 않는 경우가 생긴다.
예를 들어 800원을 거슬러 줘야 하는데 화폐 단위가 500원, 400원, 100원인 경우를 생각해 보자. 그리디 알고리즘으로 풀이한다면 800원을 거슬러 주기 위해서는 500원 동전 한 개, 100원 동전 세 개로 총 네 개의 동전이 필요한 데 반해 실제 필요한 최소 동전의 개수는 400원 동전 두 개이다.
이 문제는 결국 큰 단위의 거스름돈이 작은 단위의 거스름돈의 배수가 되지 않기 때문에 그리디 알고리즘의 두 번째 조건을 만족하지 못한다. 따라서 이런 경우는 다이나믹 프로그래밍DP과 같은 다른 알고리즘으로 해결해야 한다.
4. 그리디 문제의 판별법
앞서 서술했듯 그리디 알고리즘의 유형이 매우 다양하기 때문에, 문제를 마주쳤을 때 뚜렷한 문제 유형이 파악되지 않으면 그리디 알고리즘으로 풀 수 있는지 의심해봐야 한다. 만약 그리디 알고리즘으로 해결할 수 없을 것 같다면, 이후에 다이나믹 프로그래밍이나 그래프 알고리즘 등으로 풀이가 가능한 지 고민해보자.
5. 참고
- 나동빈, 『이것이 취업을 위한 코딩 테스트다 with 파이썬』, 한빛미디어(2020), p86-91.